Practical Mega Clusters

Overview

In a previous post we covered the different types of DVT clusters and discussed how to break down centralized clusters by using a concept called Mega-Cluster(MC). An MC is a cluster-of-clusters, coordinating different entities into using each other’s operators for their own validators; doing so decentralizes (operationally) how validators on Ethereum are run.

Stake centralization, incentives and correlated risks have been discussed extensively in the ethereum community(here, here, here and here), as a serious concern about the safety and robustness of ethereum under various attack vectors.
Intuitively, most issues are reduced the more “decentralization” is introduced. For our purposes, decentralization simply means what entities operate a validator. Operating a validator means making thousands of decisions a year on what to vote, distributing those decisions makes the overall ethereum network more resilient.

There are other 2 issues regarding decentralization which are not covered by MCs: key generation and withdrawal credentials.

A big challenge still remains: how does the MC manage inequalities between operators? That is, if operator O1 needs to run more validators than O2, then how will the MC manage that? In other words, how do we solve dynamic capacity needs?

Problem statement

There is a group of operators O and a group of validators V belonging to a group of entities E such that:

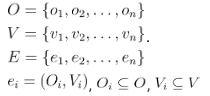
Each entity might have a different number of operators and validators. MC capacity is defined as the amount of new validators able to be added by the existing operator set:

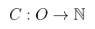
The problem is how to make entities add more operators to make C grow with demand.

Practical Mega-Cluster

Incentivizes

Incentives can make entities “want” to add more operators, dynamically adding capacity to the MC.

When capacity is “low” we can encourage an entity to register a new operator (contributing capacity), in return it will receive a share of future rewards, which is represented by a special token.
r(C) represents how many tokens an entity gets when registering an operator.
C0 is the target capacity the MC should always have

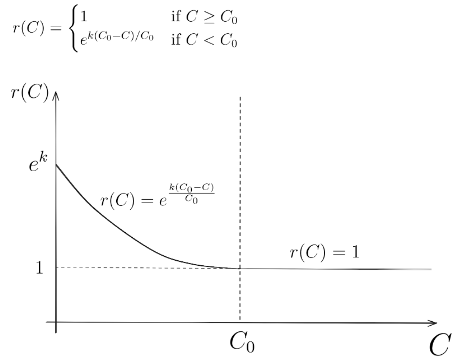
Incentives can come from various sources. One suggestion can be to use SSV’s incentivized mainnet rewards for registered validators to subsidize rewards. That will require no out-of-pocket payment from the entities.

Calculating Capacity

We can use a simple greedy algorithm to calculate capacity

library MegaClusterCapacity {
 function greedyClusterCalculation(
   uint[] memory operator_capacity
 ) internal pure returns (uint) {
   uint ret;
   uint[] memory capacities = operator_capacity;

   for (uint i=0 ; i <= capacities.length — 4; i++) {
     uint[] memory sorted = sortDesc(capacities);
     
     // add to capacity
     ret += sorted[3];

     //reduce for next iteration
     sorted[0] -= sorted[3];
     sorted[1] -= sorted[3];
     sorted[2] -= sorted[3];
     sorted[3] -= sorted[3];

     // set and iterate
     capacities = sorted;
    }

    return ret;
   }

  function sortDesc(
     uint[] memory values
   ) internal pure returns (uint[] memory ) {
   uint length = values.length;

   for (uint i = 0; i < length; i++) {
     for (uint j = 0; j < length - 1; j++) {
       if (values[j] < values[j + 1]) {
           uint temp = values[j];
           values[j] = values[j + 1];
           values[j + 1] = temp;
         }
       }
     }
     return values;
   }
}

Equilibrium

Operators can support up to T validators each.
An entity’s equilibrium can be defined as:

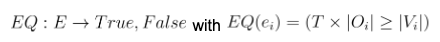
The practical purpose of a mega cluster in equilibrium is that all entities put in and take out exactly the same amount of capacity.
Entities in the mega cluster should strive for an equilibrium such that it won’t “cost” them anything to use it. r(C) changes such that it’s worthwhile for them to move the mega cluster back to equilibrium by adding/ removing operators or validators.

Example

A mega cluster is constructed out of 5 different entities, holding different capacities depending on T.
At different times, registering more capacity by one of them will result in different ration r(C), ultimately resulting in different reward shares between them.

150 validators (fig. 2) will generate ~$197K in IM rewards (ETH APR 3.7%, ETH/USD $3,700). Allocating 10% of that for contributor incentivization will result in ~$20K/ year rewards for operators willing to add operators when r(C) > 1

Figure 1 — capacity per entity and time

Figure 2 — r(C) as a function of time

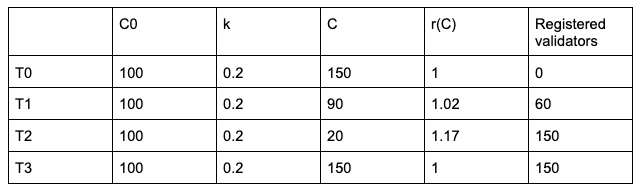
A mega cluster in equilibrium (all entities contribute exactly the same amount of capacity and consume equal capacity amounts) will result in all participating entities consuming and “paying” exactly the same.

A mega cluster, not in equilibrium, will result in some entities consuming more and some paying more (for capacity).

Solidity Code

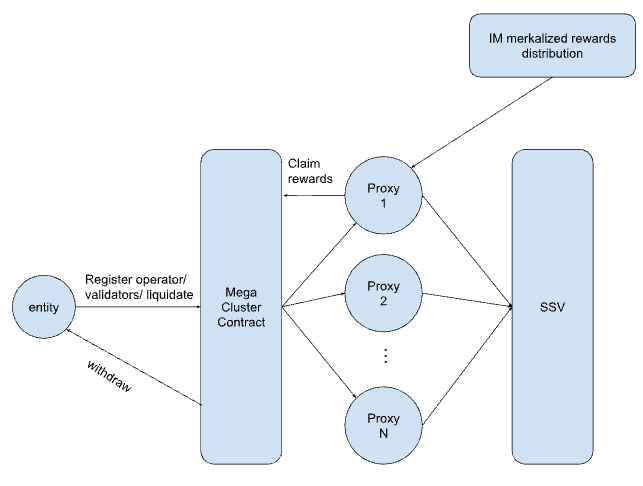
Here is a V1 version of a Practical-Mega-Cluster solidity contract that wraps around the main ssv.network contracts.

It uses the incentivized mainnet rewards as the incentive layer for registering more operators, taking 10% out of those rewards and leaving them in the contract as a rewards pool.
Each entity has a separate “proxy” contract deployed which makes perfect separation between them such that one entity cannot execute operations for another entity (in the ssv contracts).

Figure 3 — diagram of the solidity code for a practical mega cluster

Next steps

Practical mega clusters seem to be solving the coordination problem between participating entities. The overhead for the V1 contracts seems reasonable which makes the next step be testing on testnet.

I’m confident that by EOY we can have thousands of validators running as an MC, by next year tens of thousands!